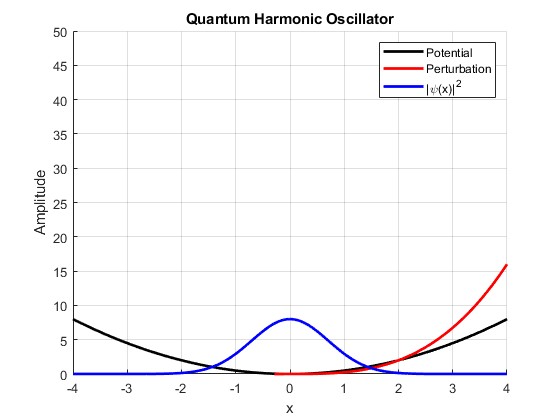
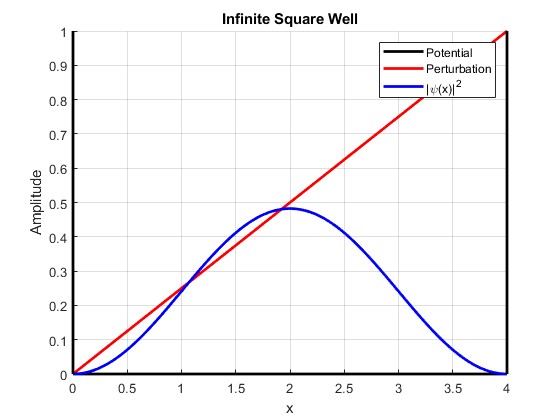
This information was completed as part of an assignment for PHYS3111 Quantum Mechanics at UNSW. I have tried to present this information in a very accessible manner for someone who does not have experience with Quantum Mechanics, feel free to skip any equations and just look at the pretty graphs.
Recommended previous knowledge:
The configuration interaction (CI)is a variational method for obtaining solutions for the Schrodinger equation (non-relativistic). The basic variational method involves guessing an arbitrary wavefunction and approximating the energy based upon that. However, in the CI method we express the (approximate) wavefunction as a linear combination of basis states. Recalling that in quantum mechanics our basis' are complete, therefore we can say that the true wavefunction, is the sum over all the basis (eigen) states. All that remains is to solve for the coefficients of each basis state as below:
\[ \psi = \sum_i c_i \ket{i} \]Here, \(\psi\) is the true wavefunction, \(c_i\) are the coefficients and \(\ket{i}\) is the ith basis state for our chosen basis. The more states we use (the higher i goes), the more accurate our wavefunction becomes to the true wavefunction. This form of the variational method is well suited for computational analysis. Further proofs can be found in various textbooks (and is left as an excercise for the reader), but it ultimately boils down to the following equation:
\[ \sum_i H_{ij}c_j = \epsilon c_i \]
Here in this equation, \(c_j\) and \(c_i\) are the jth and ith coefficients, \(\epsilon\) is the energy of the system, and \(H_{ij} = \bra{i}\hat{H}\ket{j}\). The inner product of the Hamiltonian operator with the ith and jth basis states.
We can imagine this as an eigenvector question where \(H_{ij}\) is the ijth entry. Then all that remains is to find the eigenvectors (which a computer can do quite easily) and then those are the different coefficients of our basis states. As you can imagine, the higher the amount of basis states used, the better, however we run into computer issues, would you believe it! My, not at all optimised, code written in Matlab takes about an hour to calculate all the coefficients from 1 basis state up to 15. I'm sure there are many ways to speed this process up (there's a lot of loops), it ran fine enough for the purposes of this page. Let's make the magic happen!
Now all we need is the following:
The code I used will be availible for download at the bottom so you can play around with it for yourself. If you have any questions about anything written here, feel free to drop me a message via LinkedIn!